Zero Vector Mathematical Definition
2Existence of a zero vector. The null vector or is the vector with length zero.

Vector In Math Definition Multiplication Examples Video
Consider again the eigenvalue equation Equation.

Zero vector mathematical definition. U v v u u v w u v w There exists an element 0. The direction of the zero vector is undefined. Sub0 W is nonempty.
Written out in coordinates the vector is 000 and it is commonly denoted or 0 or simply 0. Note that a vector that has a magnitude of. Then a vector is by definition an element of a vector space.
Zero Vector The vector w 00 w 0 0 that we saw in the first example is called a zero vector since its components are all zero. In mathematics you define a vector space V over a field like real numbers etc F to be as a triplet V where denotes the vector addition and denotes the scalar multiplication which has the following properties. 1Associativity of vector addition.
The zero vector is then the provably unique vector in a given vector space which behaves neutrally with respect to addition of vectors. Well the span of a set A X is defined as the smallest vector subspace of X that contains A. The zero vector belongs to W.
Adding the zero tensor is equivalent to the identity operation. Be careful to distinguish 0 the number from 0 0 the vector. The zero tensor of order 1 is sometimes known as the zero vector.
While the definition of an eigenvector used in this article excludes the zero vector it is possible to define eigenvalues and eigenvectors such that the zero vector is an eigenvector. The divergence of a vector field Fx at a point x0 is defined as the limit of the ratio of the surface integral of F out of the surface of a closed volume V enclosing x0 to the volume of V as V shrinks to zero. Then W is a subspace of V if and only if the following conditions hold.
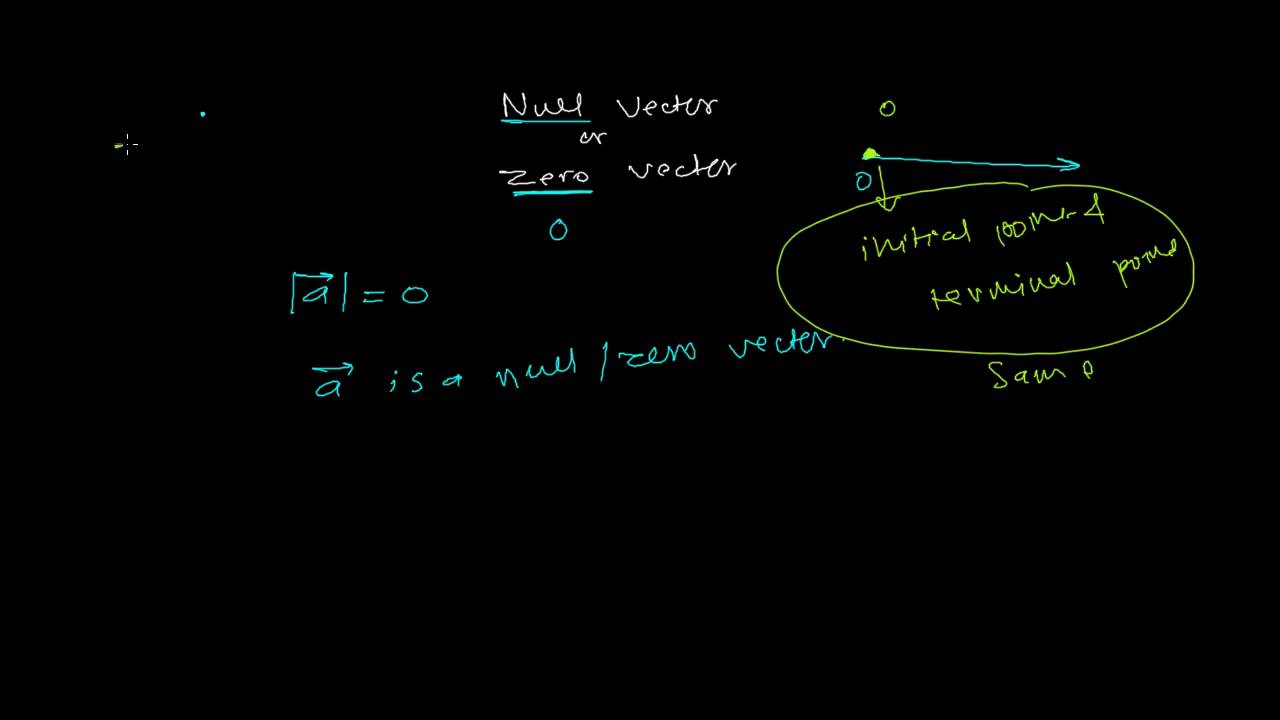
A 00 and A 0 are different ways of writing zero vectors. Zero vectors are often denoted by 0 0. A vector of which all the components are zero.
A vector is called a zero vector if its magnitude is zero. It should be emphasized that the precise name of the zero vector is highly sensitive to the vector space structure. That is the subset of V consisting of all those elements of V that are mapped by T to the element 0 W.
U v w u v w for all uvw2V. Unlike any other vector it does not have a direction and cannot be normalized ie. If 0 W is the zero vector of W then the kernel of T is the preimage of the zero subspace 0 W.
There is a vector in V written 0 and called the zero vector which has the property that u0 ufor all u2V 3Existence of negatives. Alternatively the span of A is the intersection of all vector subspaces that contain A. If W is a vector space with respect to the operations in V then W is called a subspace of V.
For any sequence of closed regions V1 V2 V3. Taking a tensor product of any tensor with any zero tensor results in another zero tensor. Enclosing x that approaches zero volume.
The zero vector is the unique vector having zero length. Zero vector as an eigenvector. It also has no specified direction.
Let V be a vector space with operations and and let W be a subset of V. Let V and W be vector spaces over a field or more generally modules over a ring and let T be a linear map from V to W. Since all vector subspaces contain it is clear that 0 which is the smallest vector subspace at all must be the span of.
In mathematics the zero tensor is a tensor of any order all of whose components are zero. The vectors in a subset S v 1 v 2 v k of a vector space V are said to be linearly dependent if there exist a finite number of distinct vectors v 1 v 2 v n in S and scalars a 1 a 2 a n not all zero such that a 1 v 1 a 2 v 2 a k v k 0 where zero denotes the zero vector. A zero vector starts and ends at the same point which means it has the coordinates 00.
That is what the zero vector is. For every u2V there is a vector in V written uand called the negative of u which has the property that u.

Types Of Vectors Collinear And Equal Vectors Videos Solved Examples
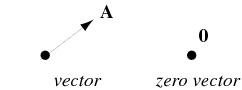
Zero Vector From Wolfram Mathworld
An Introduction To Vectors Math Insight
Zero Vector Null Vector Youtube
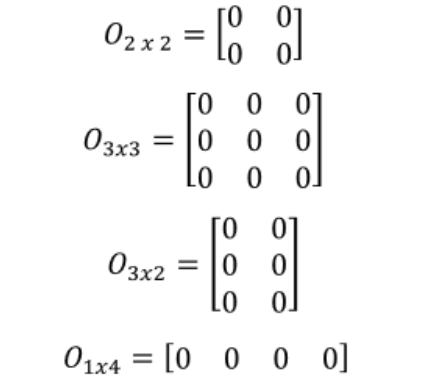
Definition Of A Zero Matrix Studypug
Vectors In Maths Euclidean Vector Examples Applications
The Zero Transformation Mathonline
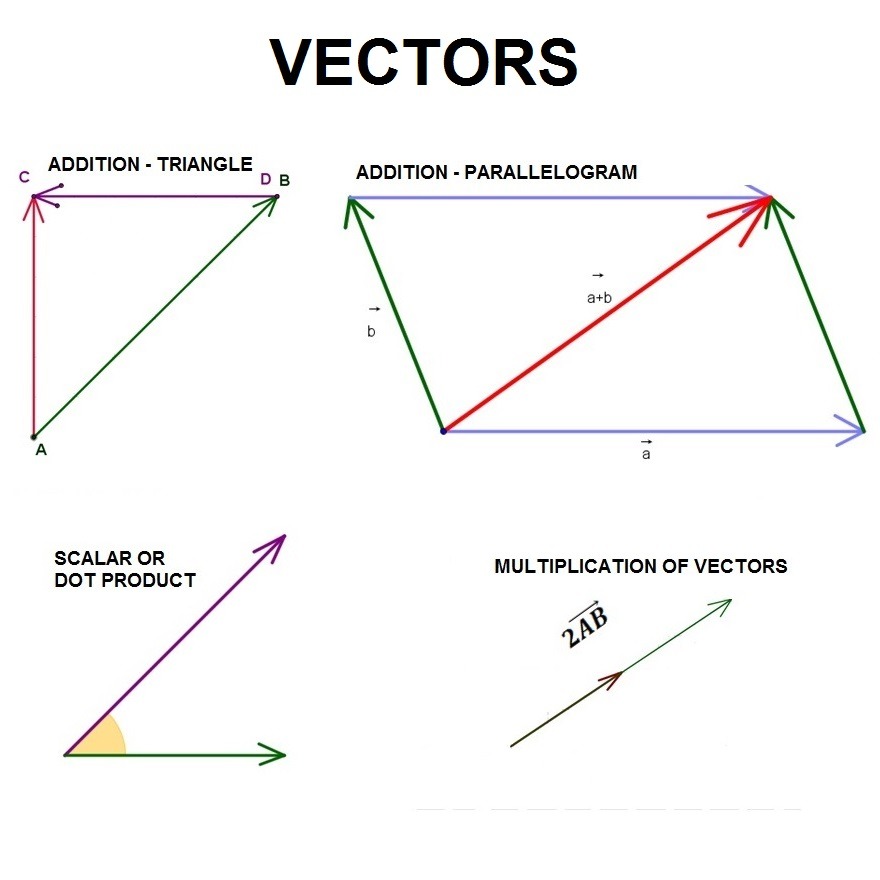
Vectors Direction Orientation Addition Multiplication Scalars
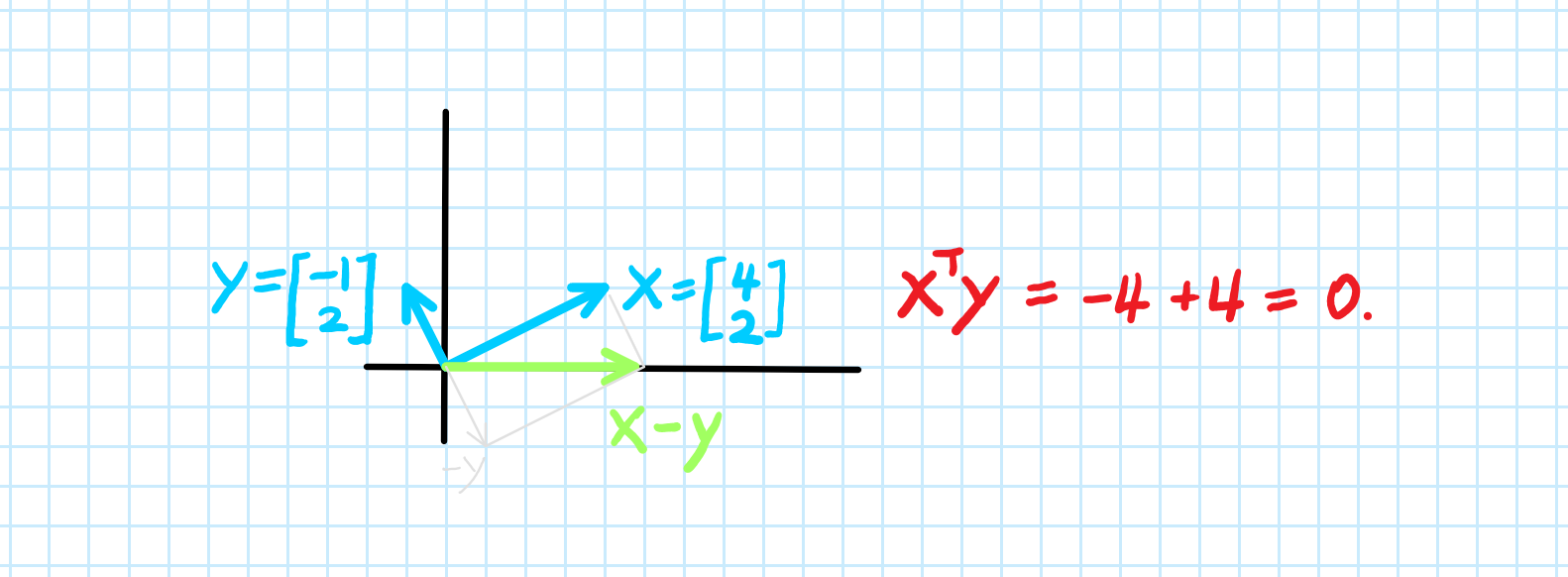
Why Is The Dot Product Of Orthogonal Vectors Zero By Aerin Kim Towards Data Science

Vector In Math Definition Multiplication Examples Video
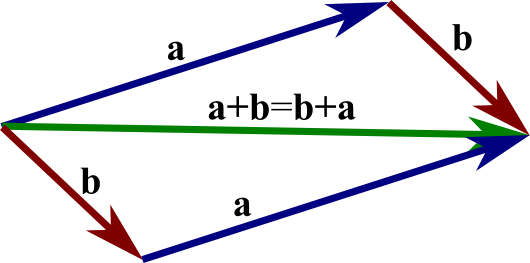
An Introduction To Vectors Math Insight

An Introduction To Vectors Math Insight

Vectors In Two And Three Dimensional Cartesian Coordinates Math Insight

An Introduction To Vectors Math Insight

Linear Algebra Chapter 4 Vector Spaces Ppt Download
What Is A Null Or Zero Vector Youtube

About Definition In Linear Algebra Concerning Empty Subset Of Vector Space Mathematics Stack Exchange

An Introduction To Vectors Math Insight

Scalars And Vectors Definition Types Concepts Videos And Examples